A legújabb olvasnivalók
Mindenkinek ajánljuk
Kínai csirkesaláta: egy amerikai klasszikus újragondolva
Hogyan vált egy hollywoodi kínai éteremből induló recept világszerte kedvelt fogássá, és hogyan készítheted el saját konyhádban – tudományosan megalapozott, mégis szórakoztató utazás egy tányér saláta körül Képzelj el egy helyet, ahol Cary Grant ugyanazt az ételt fogyasztja, amit később az édesanyád is elkészít a vasárnapi ebédre. Képzeld el, ahogy…
A 20-perces szabály – így csökkentheted a kalóriabevitelt erőfeszítés nélkül
Képzeld el, hogy van egy eszköz, ami csökkenti az elhízás kockázatát, javítja az emésztést, növeli az ételek élvezeti értékét, és még stresszoldó hatása is van. És a legjobb? Teljesen ingyenes, mindig nálad van, és most azonnal elkezdheted használni. Mi az? A saját, tudatosan lelassított étkezési ritmusod. Igen, jól olvastad. A…
Miért váltanak egyre többen szilárd samponra?
A legmegrázóbb felismeréseim egyike egy apró, szilárd sampon korong formájában érkezett. Nem egyszerűen arról, hogy hogyan ápolom a hajam, hanem arról, mennyi mindent bonyolítunk túl az életünkben – pusztán azért, mert így szoktuk meg. Szilárd sampon: Az út a szkepticizmustól az átalakulásig Emlékszem, ahogy a fürdőszobai polcomon sorakoztak a különböző…

A FELELŐSSÉGGEL GONDOLKODÓK LAPJA
Ha tudatos olvasónak vallod magad, akkor ez az lap Neked szól!
A Zöld Újság több mint húsz éve egyet jelent aze gészséges életmóddal! Fizess elő a havonta megjelenő digitális magazinra mindössze 990 forintért!
Megosztásra érdemes
Csend és szavak között: Miért nem értjük egymást igazán?
Mit keresnek a férfiak a csendben? És mit próbálnak elmondani a nők a szavaikkal? Nem, ez nem egy újabb önsegítő cikk, amely instant válaszokat ígér az érzelmi távolságokra. Ez egy olyan írás, amely megpróbál a felszín alá nézni – oda, ahol a modern férfi és nő közötti kapcsolatot a félreértések hálója tartja fogva. Egy olyan világban, ahol a ‘mondd el,…
Népszerű
Amit a nyelved elárul: mesterséges intelligencia az ősi gyógyítás nyomában
Amit a nyelved elárul Mesterséges intelligencia az ősi gyógyítás nyomában Évezredeken át a keleti gyógyítók úgy olvastak a…
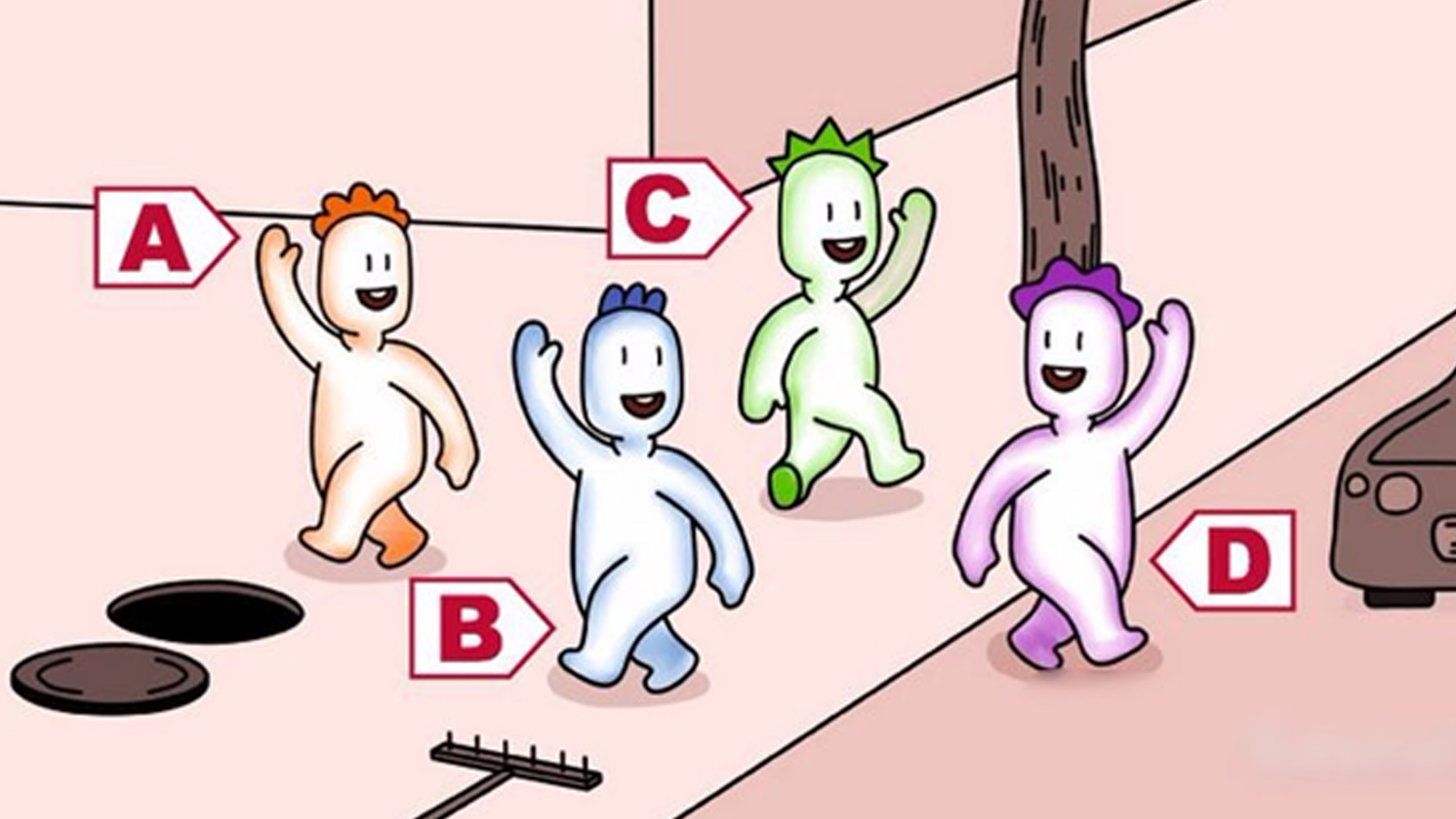
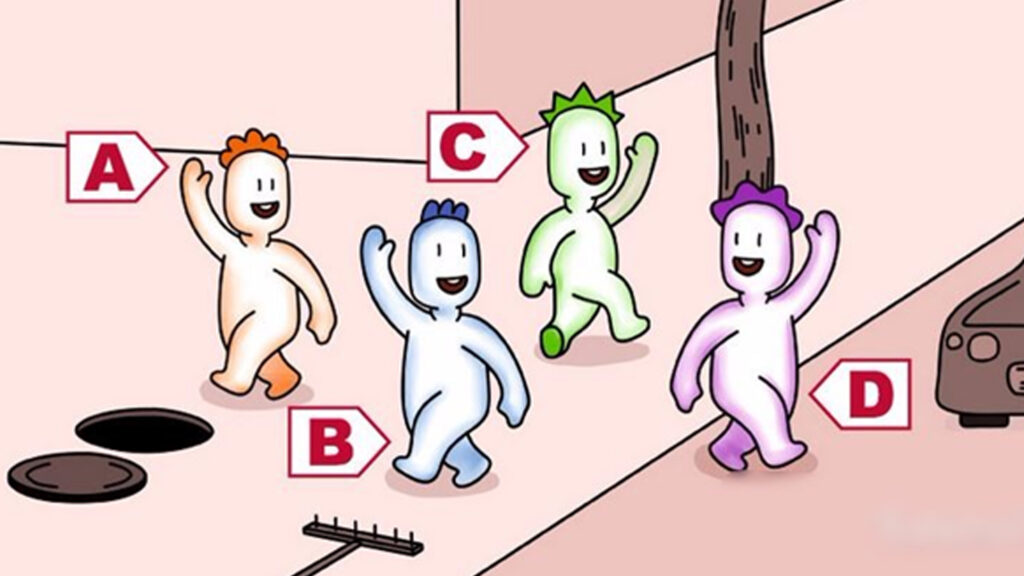
Félelmeid tükrében: Egy izgalmas személyiségteszt
Félelmeid tükrében Egy személyiségteszt, ami meglepő módon az erősségeidet mutatja meg A négy barát közül szerinted melyik szenved…
Fűszermesék – Merüljünk el az ízek tengerében!
A magyar konyha ízvilágát nehéz elképzelni a jellegzetes fűszereink nélkül. Ezek a növényi eredetű ízesítők nem csupán az…